from IPython.display import Audio, FileLink, display
import pandas as pd
Als erstes lesen wir mit [Read] in PRAAT unsere Sprachdatei ein. Dann wählen wir "Formants&LPC->To LPC (autocorrelation)". Die anderen Verfahren, die PRAAT noch anbietet, unterscheiden sich nur geringfügig in der Methode der Berechnung der Filter-Koeffizienten. Im Einstelldialog sind besonders die Punkte "Prediction Order" (Ordnung des Filters) und "Analysis width" (Framebreite bei der Analyse) von Interesse. Diese wollen wir in dieser Aufgabe variieren. Zusätzlich zu den von PRAAT angebotenen Standardwerten von Order=16/Analysis Width=25ms (kurz: 16/25) werden wir Analysen bei Ordnungen von 10, 6 und 1 durchführen, sowie Framelängen von 50 und 100 ms untersuchen. "Time step" (die "Vorschubbreite" der Analyse) setzen wir auf denselben Wert wie "Analysis width", d.h. wir erlauben kein Überlappen von benachbarten Frames
Audio('sound/sprachsignal.wav')

Die Objekte sind als Collection gespeichert und nach dem Schema \
FileLink('lpc/lpcs.collection')
Nachdem die verschiedenen LPC-Objekte kreiert wurden, führen wir zunächst eine inverse Filterung des Sprachsignals durch, mit der wir theoretisch die "Quelle" zurückgewinnen (Sound und LPC (16/25) gemeinsam anwählen, "Filter (inverse)"). Das entstehende Signal, das auch als "Residual"-Signal bezeichnet wird, betrachten wir im Edit-Fenster. Wie unterscheiden sich die Spektren vom Original, wie ist die Restverständlichkeit der ursprünglichen Sprache? (Spektrogramme von Original und Residual-Signal ins Protokoll) Nun gewinnen wir das ursprüngliche Signal wieder zurück (Rekonstruktion), indem wir das Residuum mit dem dazugehörigen LPC-Objekt (16/25) filtern (Residuum und LPC gemeinsam anwählen, "Filter", "Use LPC Gain" nicht ankreuzen!).
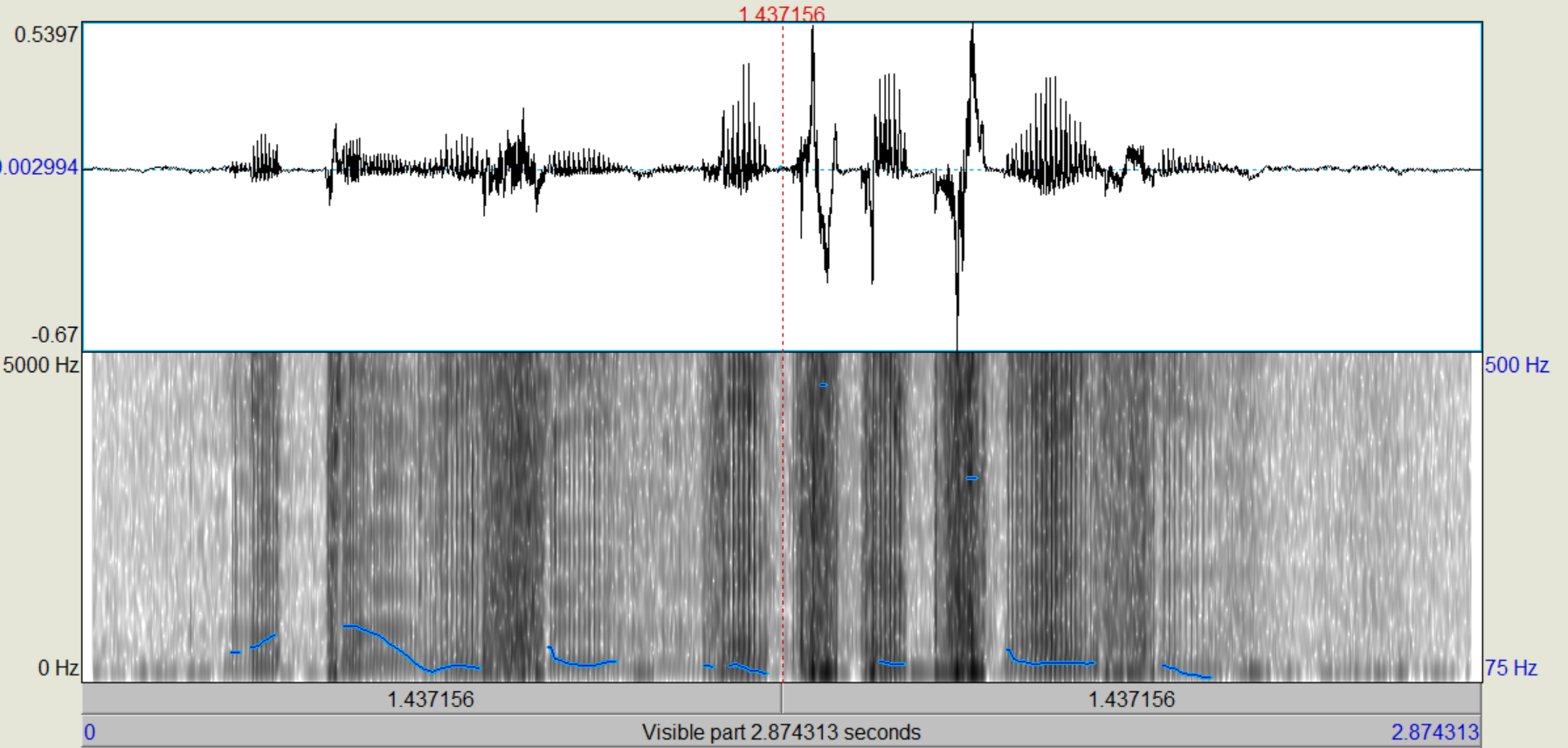
Bei dem Residualsignal kann man sehr deutlich erkennen, dass die Formanten weitestgehend aus dem Sprachsignal gefiltert wurden, sodass primär die Grundfrequenz übrig bleibt. Einige kleine Reste der Formanten konnten nicht aus dem Signal entfernt werden, aber der Einfluss dieser ist sehr gering und kann weiter vernachlässigt werden. Trotzdem ist aus der Grundfrequenz das ursprüngliche Sprachsignal weiterhin recht deutlich zu erkennen.
Audio('sound/residuum_16_25.wav')
Bei dem Residuum kann man sehr deutlich sehen, dass die Frequenzen sehrgleichmäßig verteilt sind. Die Formanten lassen sich noch knapp erahnen, wurden aber weitestgehens gefiltert. Das Sprachsignal ist noch zu erkennen, aber lange nicht mehr so dutlich. Nach der Rekonstruktion ist das ursprüngliche Sprachsignal entstanden.
Audio('sound/16_25_reconstructed.wav')
Das Residual-Signal dient uns jetzt zum Testen der anderen LPC-Objekte mit den verschlechterten Parametern. Auch hier wählen wir das Residuum und das gewünschte LPCObjekt an und filtern wieder. Vergleiche die Qualität der einzelnen Varianten mit dem Original! Wie unterscheiden sich die Beispiele, bei denen die Filter-Ordnung variiert wurde, wie solche, bei denen die Framebreite variiert wurde? Bei welcher Kombination ist die Sprachverständlichkeit nicht mehr akzeptabel?
display(Audio('sound/16_25.wav'))
display(Audio('sound/16_50.wav'))
display(Audio('sound/16_100.wav'))
Mit der Fensterlänge 25mS wurde das Sprachsignal perfekt rekonstruiert. Dies sollte auchd er Fall sein, da das Ursprüngliche Signal mit der selben Ordnung und Fensterlänge gefiltert wurde. Bei der Rekonstruktion mit Fensterlänge 100mS lassen sich bereits deutlich Fehler im rekontruierten Signal erkennen. Es wirkt, als würde das Signal stellenweise übersteuern. Im Spektrum kann man bei allen Signalen wieder die Formanten deutlich erkennen.
display(Audio('sound/10_25.wav'))
display(Audio('sound/10_50.wav'))
display(Audio('sound/10_100.wav'))
Das Ergebniss der Rekonstruktion mit einer Fensterlänge von 25mS klingt weiterhin recht sauber, wenngleich ein wenig dumpfer, als wären die hohen Frequenzen nicht perfekt wieder hergestellt wurden. Das Signal, welches mit 100mS rekonstruiert wurde weißt dazu weitere, deutliche Übersteuerungen auf.
display(Audio('sound/6_25.wav'))
display(Audio('sound/6_50.wav'))
display(Audio('sound/6_100.wav'))
Die Signale wirken wieder deutlich dumpfer, als das ursprüngliche Signal und bei zunehmender Fensterlänge treten deutlich Übersteuerungen im rekonstruierten Signal auf.
display(Audio('sound/1_25.wav'))
display(Audio('sound/1_50.wav'))
display(Audio('sound/1_100.wav'))
Die Signale, welche mit Ordnung 1 rekonstruiert wurden klingen weitestgehend wie das Residuum Signal. Im Spektogram kann man erkennen, dass die Signale mit zunehmender Ordnung weiterhin lokal übersteuern, allerdings lassen sich diese Fehler aus auditorial kaum noch erkennen.
Die Qualität der Rekonstruktion nimmt mit abnehmender Ordnung und zunehmender Fensterlänge merklich ab. Die höheren Ordnungen scheinen primär die hohen Frequenzen im Sprachsignal darzustellen, da die Signale mit abnehmender Ordnung zunehmen dumpfer wirkten. Mit zunehmender Fensterlänge treten mehr Übersteuerungen auf, vermutlich durch die Rückkopplung des Filters.
Die Datenrate lässt sich aus der Ordnung(o) und Fensterbreite(l) des LPC berechnen:
index = [[16, 10, 6, 1], [0.025, 0.050, 0.100]]
index = pd.MultiIndex.from_product(index, names=["Ordnung", "Fensterlange(s)"])
bandwidth = pd.DataFrame(index=index).reset_index()
bandwidth['Bandbreite'] = 1/bandwidth['Fensterlange(s)'] * (bandwidth['Ordnung'] + 2) * 16
bandwidth.set_index(['Ordnung', 'Fensterlange(s)'], inplace=True)
bandwidth
| Bandbreite | ||
|---|---|---|
| Ordnung | Fensterlange(s) | |
| 16 | 0.025 | 11520.0 |
| 0.050 | 5760.0 | |
| 0.100 | 2880.0 | |
| 10 | 0.025 | 7680.0 |
| 0.050 | 3840.0 | |
| 0.100 | 1920.0 | |
| 6 | 0.025 | 5120.0 |
| 0.050 | 2560.0 | |
| 0.100 | 1280.0 | |
| 1 | 0.025 | 1920.0 |
| 0.050 | 960.0 | |
| 0.100 | 480.0 |
Nun wollen wir die Anregung (Quelle) verändern. Dafür habe ich zwei Signale bereitgestellt, weißes Rauschen und einen 100Hz-Pulse Train, einen obertonreiches Signal mit Grundfrequenz 100Hz
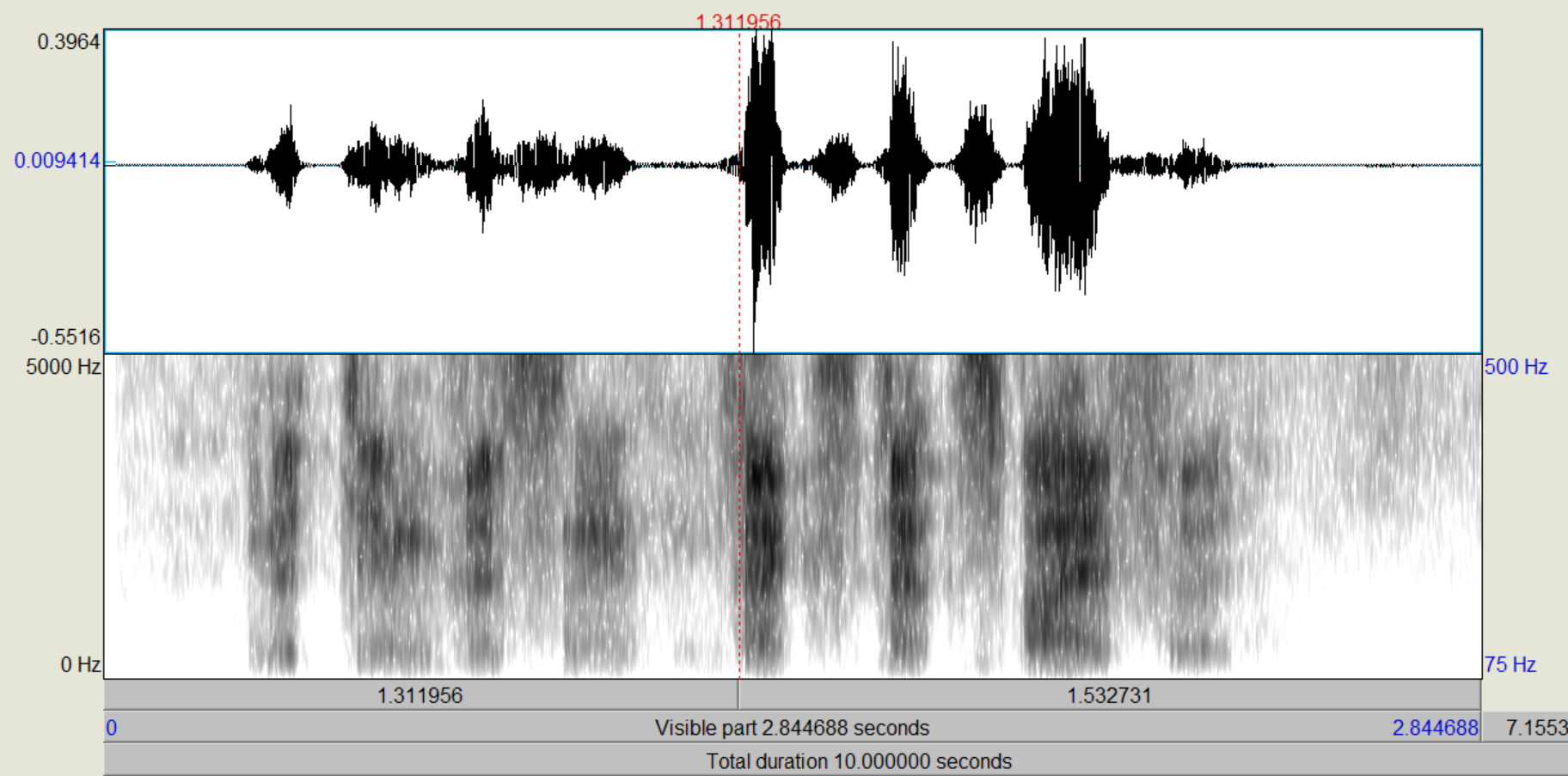
Audio('sound/whitenoise_16_25.wav')
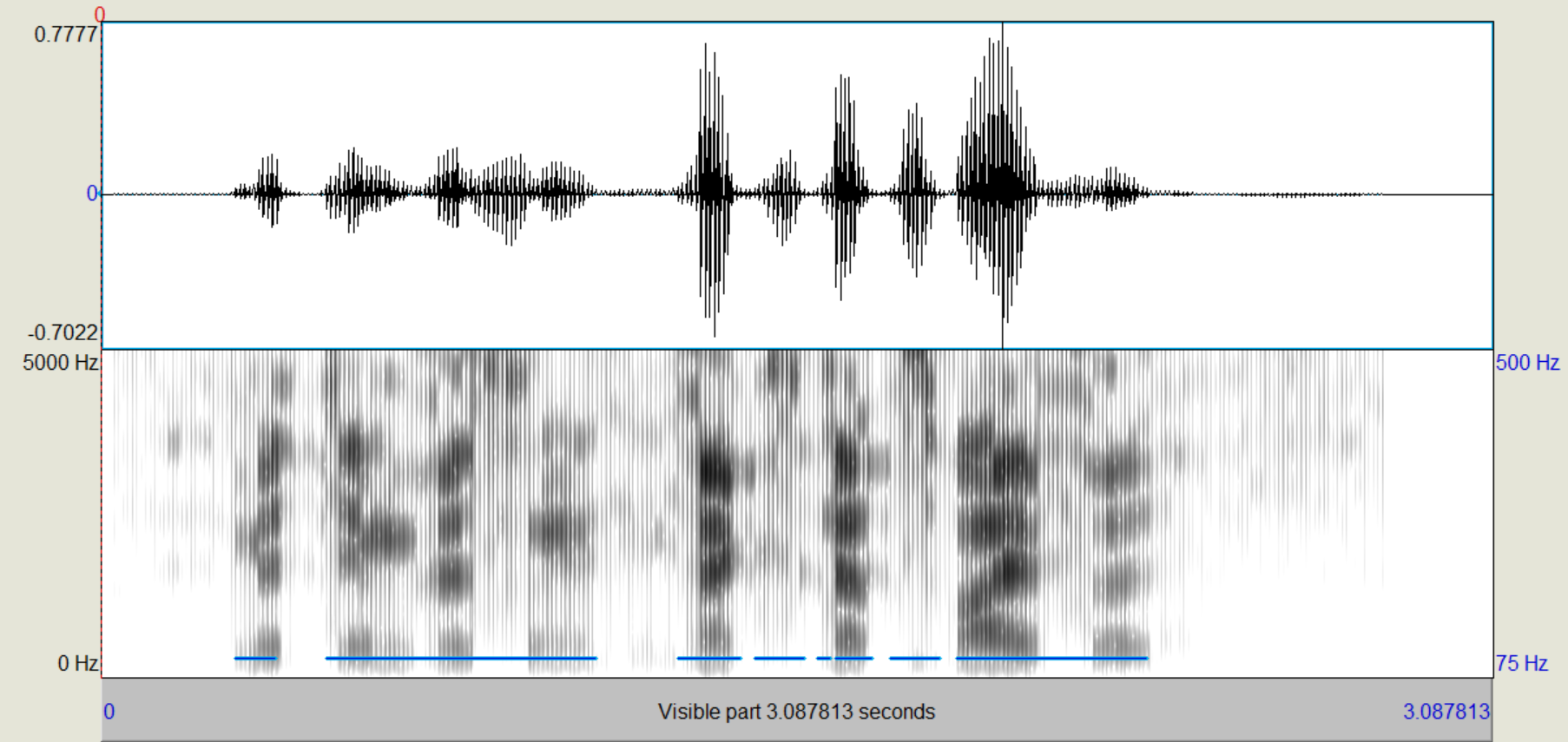
Audio('sound/pulsetrain_16_25.wav')