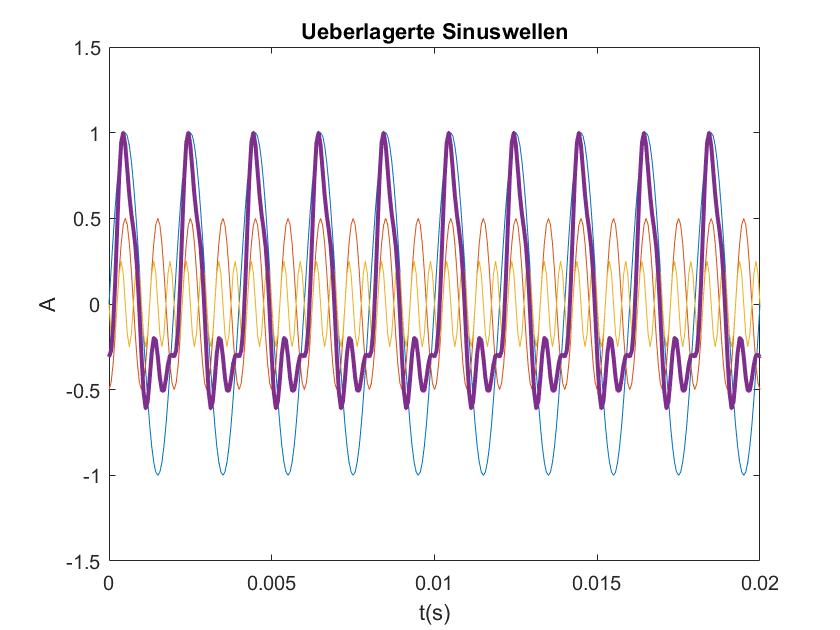
Hier sieht man die oben definierten Sinuswellen und ihre normierte Ueberlagerte
| blau | Kurve 1 |
| rot | Kurve 2 |
| gelb | Kurve 3 |
| lila | Ueberlagerte |
In dieser Übung geht es um die Fouriersynthese und -analyse. Erzeuge mit Matlab/Octave ein Sinusgemisch mit den folgenden Eigenschaften (f: Frequenz, A: Amplitude, phi Phasenwinkel):
| Kurve 1 | f1=500Hz | A1=1 | phi1=0 |
| Kurve 2 | f2=1000Hz | A2=0.5 | phi2=-pi/2 |
| Kurve 3 | f3=2000Hz | A3=0.25 | phi3=pi |
und einer Dauer von 5 s. Zeichne das Sinusgemisch mit plot im Bereich t=0-20ms. Dabei soll auf der x-Achse die Zeit in ms abgetragen sein. Gibt die Schwingung als Wave-Datei mit audiowrite aus, und zwar mit einer Abtastfrequenz fa von 16kHz und einer Auflösung von 16bit. Dabei skalieren, um Clipping zu vermeiden. Berechne die Fouriertransformation der Sinusschwingung mit der Funktion fft und stelle das ermittelte Amplitudenspektrum mit plot dar. Auf der x-Achse soll dabei die Frequenz in Hertz abgetragen werden dar und zwar zunächst für den Bereich zwischen 0 und Abtastfrequenz fa. Was fällt beim Betrachten des Spektrums auf?

Hier sieht man die oben definierten Sinuswellen und ihre normierte Ueberlagerte
| blau | Kurve 1 |
| rot | Kurve 2 |
| gelb | Kurve 3 |
| lila | Ueberlagerte |
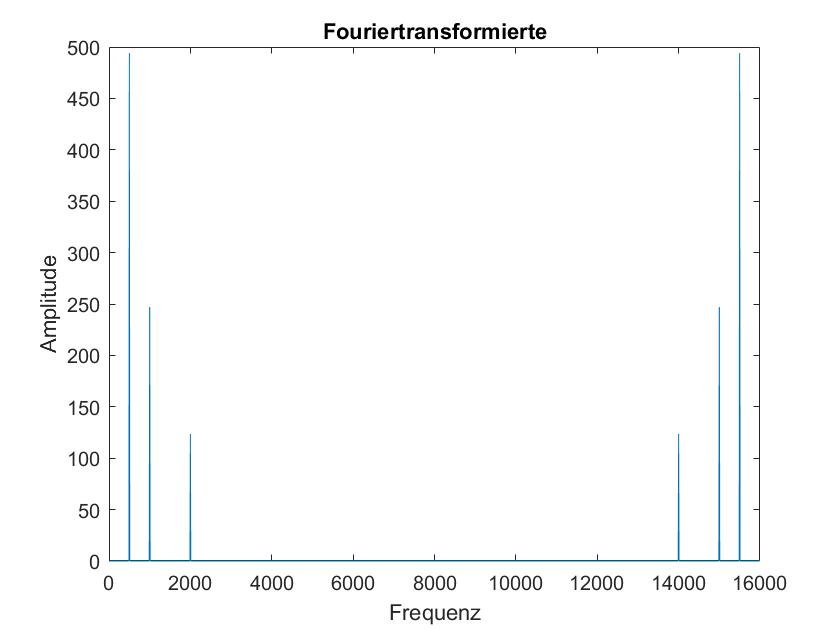
Hier sieht man die, mit der Fast Fourier Transformation, transformierte des oben gezeigten Signals
Zunaechst kann man sehr deutlich die vier Dirac Stoesse an den Frequenzen f1, f2 und f3 sowie die Einfluesse deren Amplituden sehen. Dazu faellt auch auf, dass gespiegelt sind an der Haelfte der Frequenzaufloesung. Daher kann man mit der FFT nur die Einfluesse von Frequenzen unter der Haelfte der Frequenzaufloesung analysieren
Variiere dabei die Framelänge zwischen 50ms, 100ms, 500ms, 1 s und 5 s. Welche Frequenzauflösung delta f erhältst du für die verschiedenen Framelängen? Zoome nun in den Bereich 0 bis 4 kHz hinein. Was fällt beim Spektrum bei der Variation der Framelänge auf? Wie kann man sich diesen Unterschied erklären?
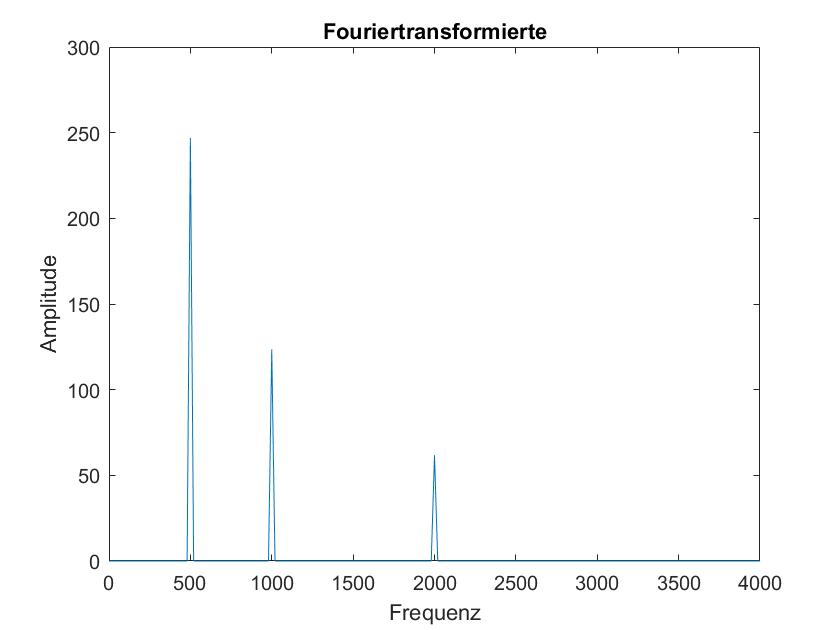
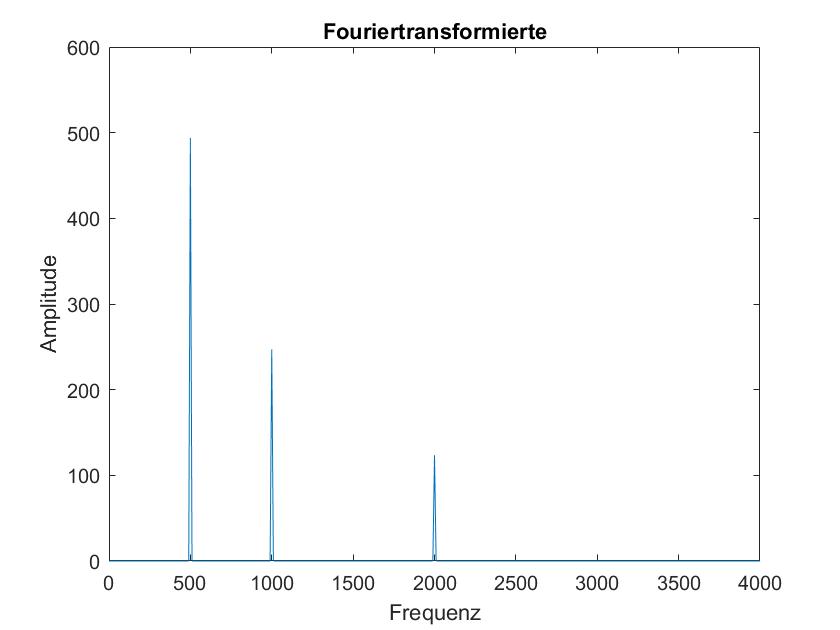
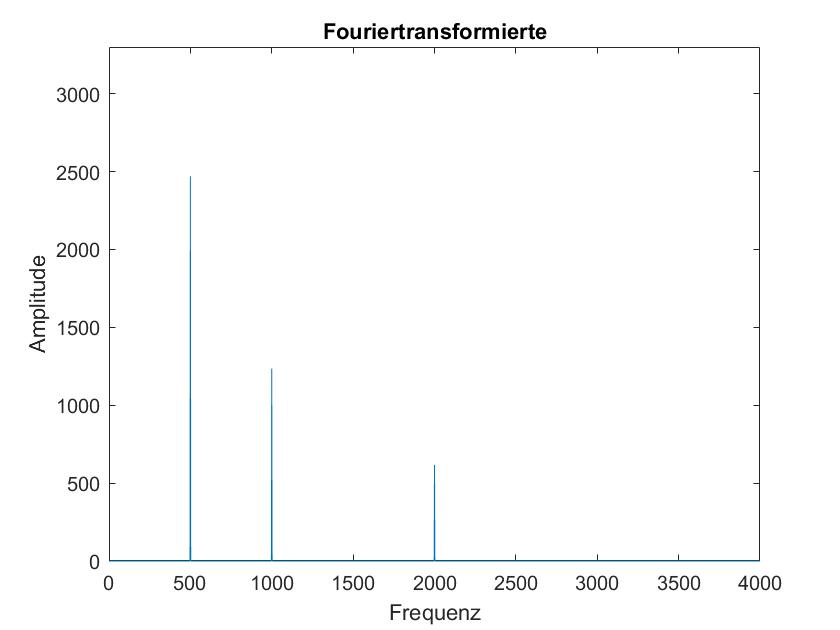
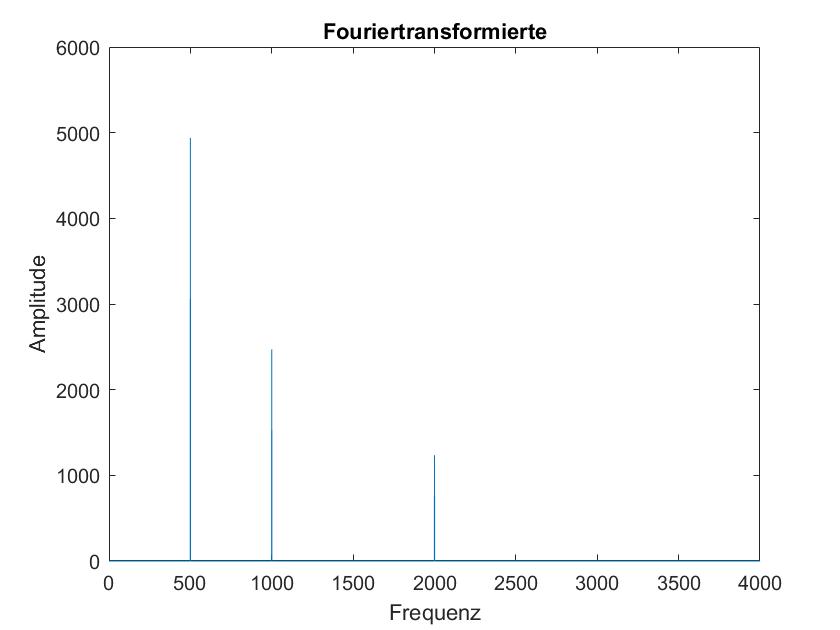
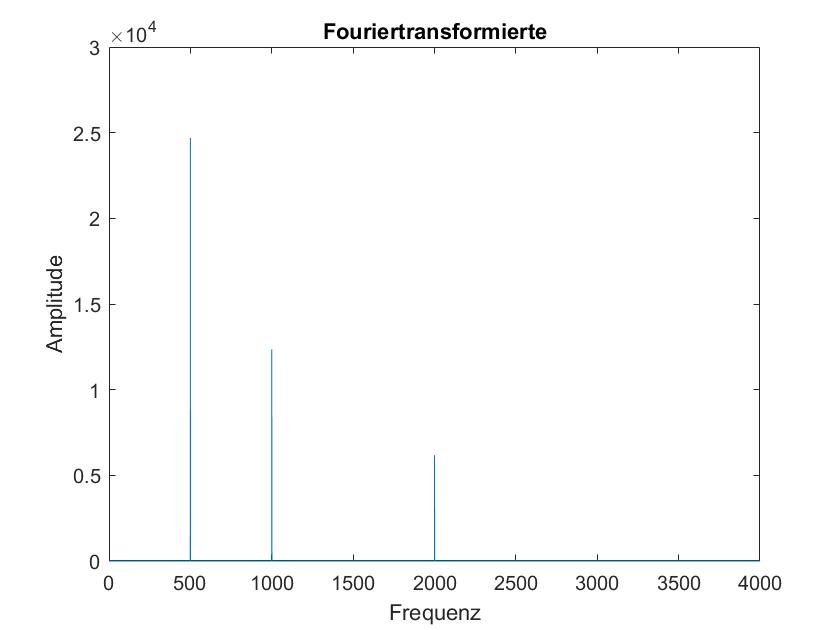
In diesen 5 Bildern sind die Fourier Transformierten des obigen Signals mit den Frame Laengen 50ms, 100ms, 500ms, 1s und 5s dargestellt. Hierbei faellt auf, dass bei einer kleineren Frame Laenge die Dirac Stoesse an den Frequenzen nicht so genau sind wie bei den groesseren Frame Laengen. Zudem steigt mit der Frame Laenge auch der Amplitudenanteil der Frequenzen. Dies liegt vermutlich daran, dass bei einer groesseren Frame Laenge mehr Signalwerte zum aufaddieren bereitliegen, daher sollte man eventuell die Ergebnisse der FFT abhaengig von der Frame Laenge normieren.
| Frame Length | delta f |
|---|---|
| 50ms | 20 |
| 100ms | 10 |
| 500ms | 2 |
| 1s | 1 |
| 5s | 0.2 |
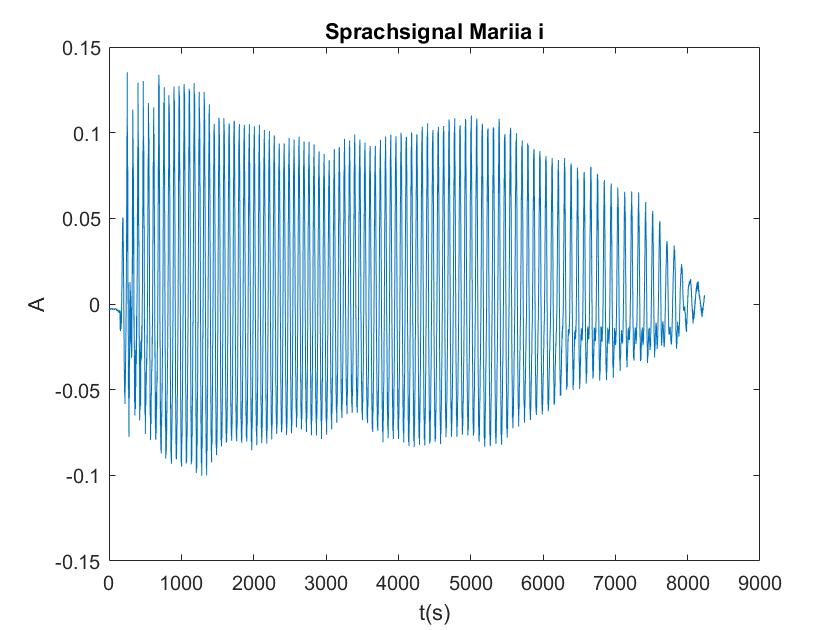
| Mariia a | Mariia i |
|---|---|
|
|
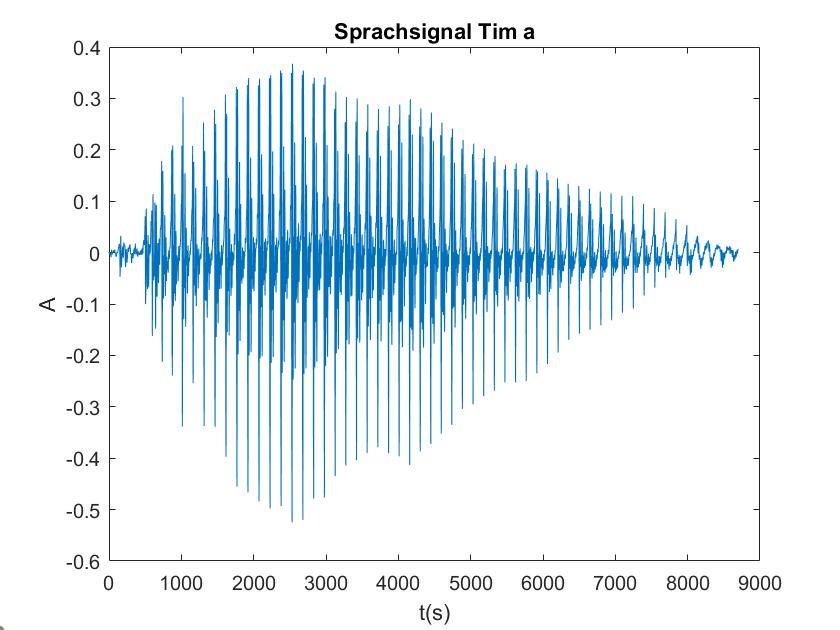
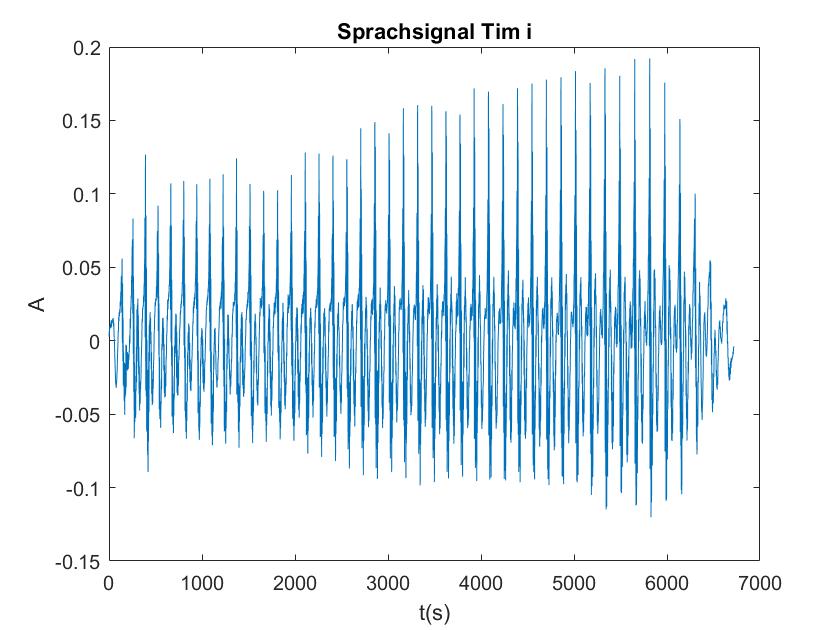
| Tim a | Tim i |
|
|
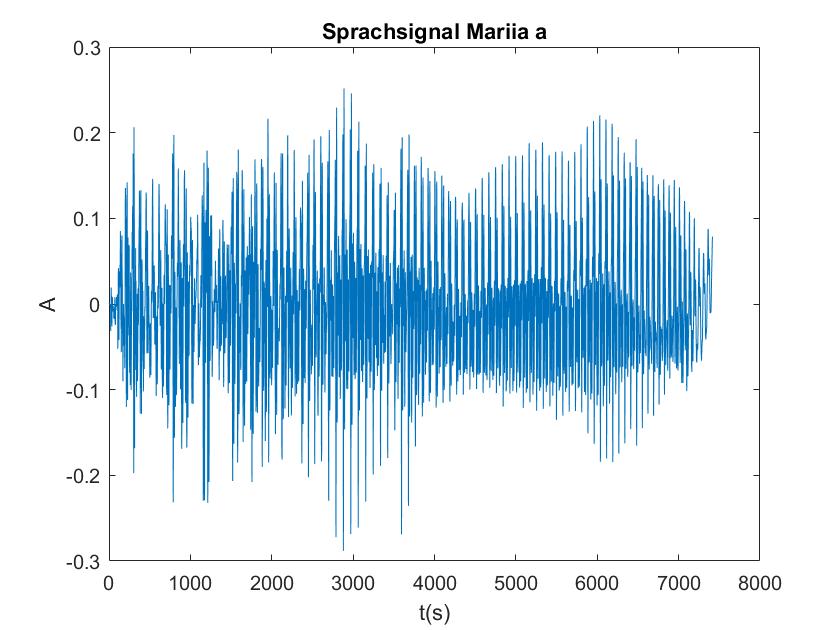
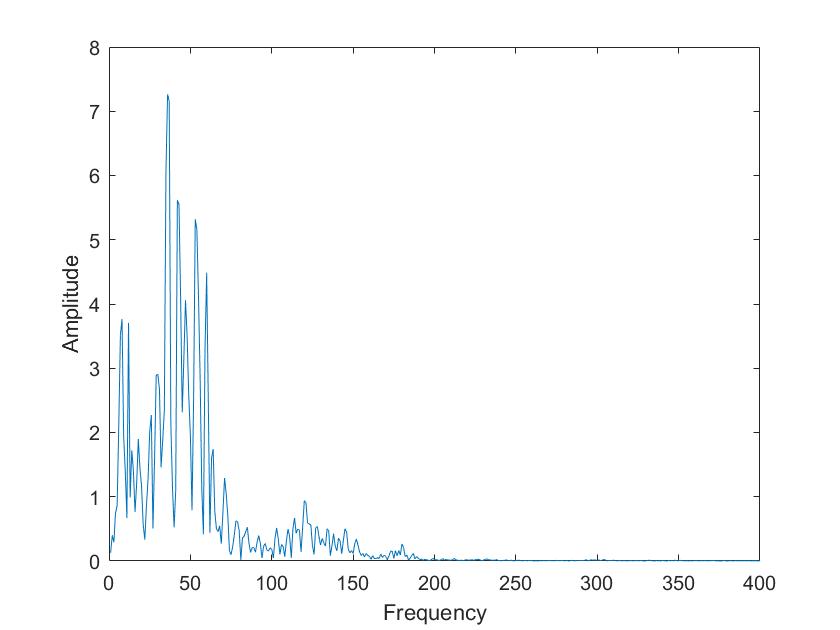
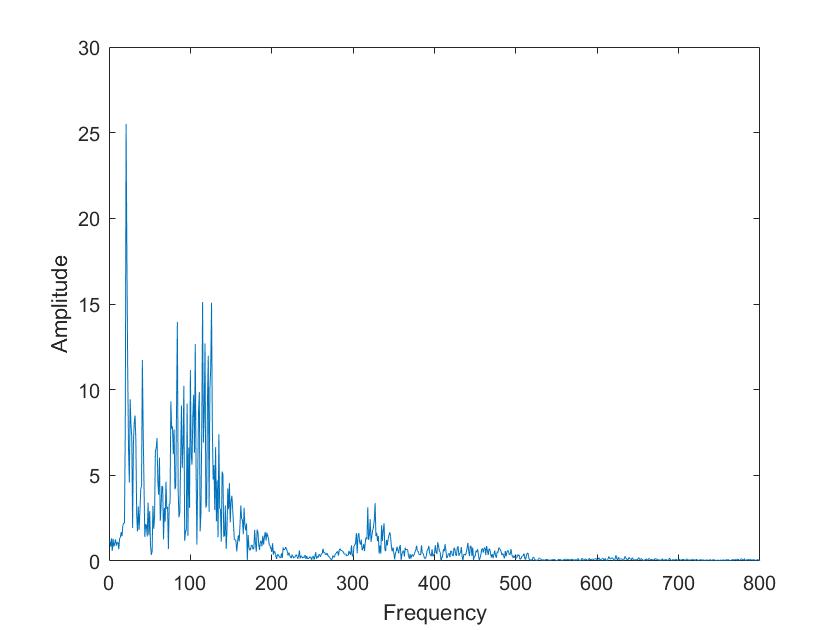
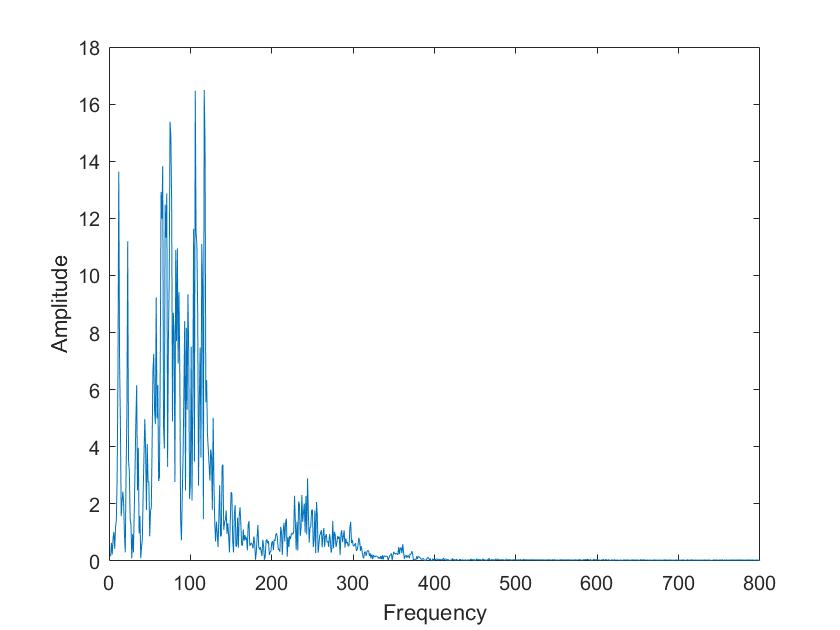
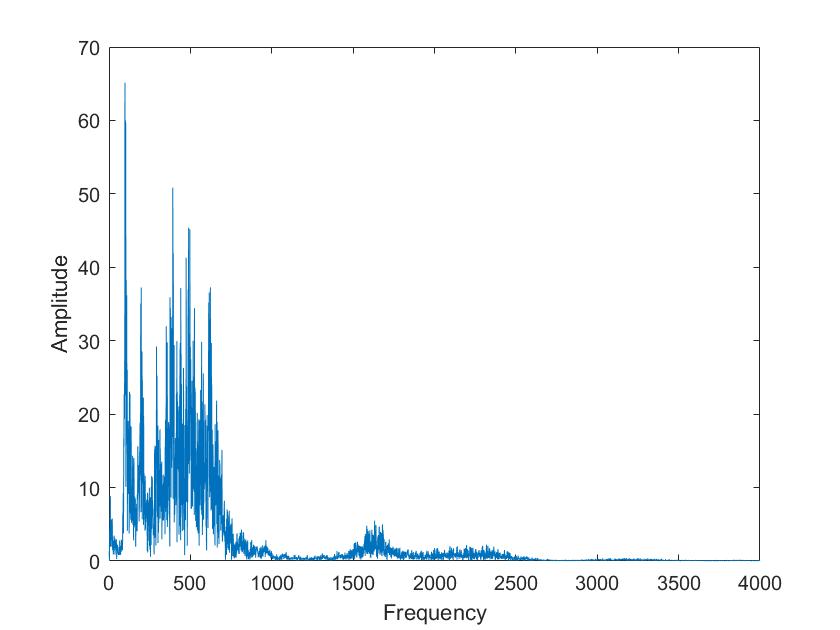
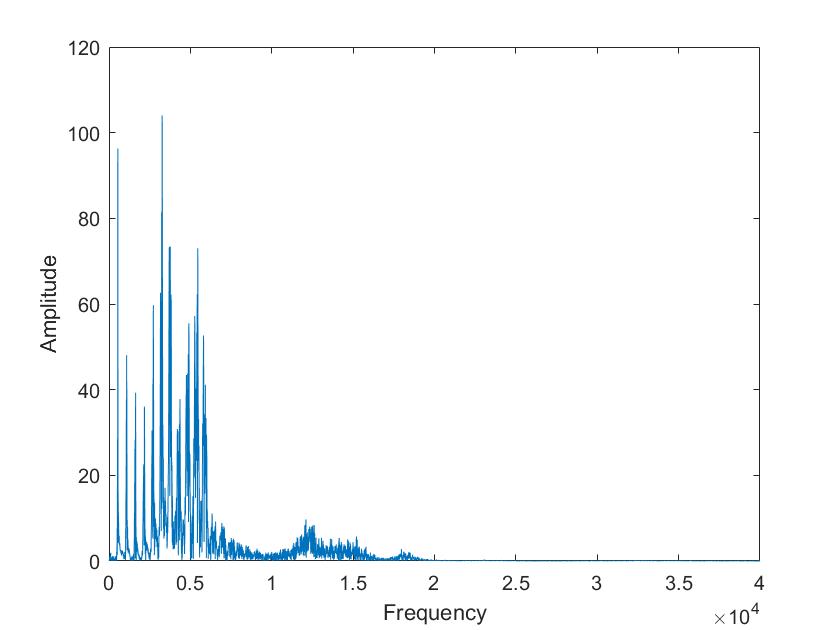
Lies die Datei mit wavread in deinem Matlab-Programm ein. Berechne auch von diesem Signal die Fouriertransformation, diesmal mit Framebreiten von 50ms, 100ms, 500ms, 1 s. Wie unterscheiden sich die Vokale in ihrem Spektrum vom Sinusgemisch und wie unterscheiden sie sich voneinander?
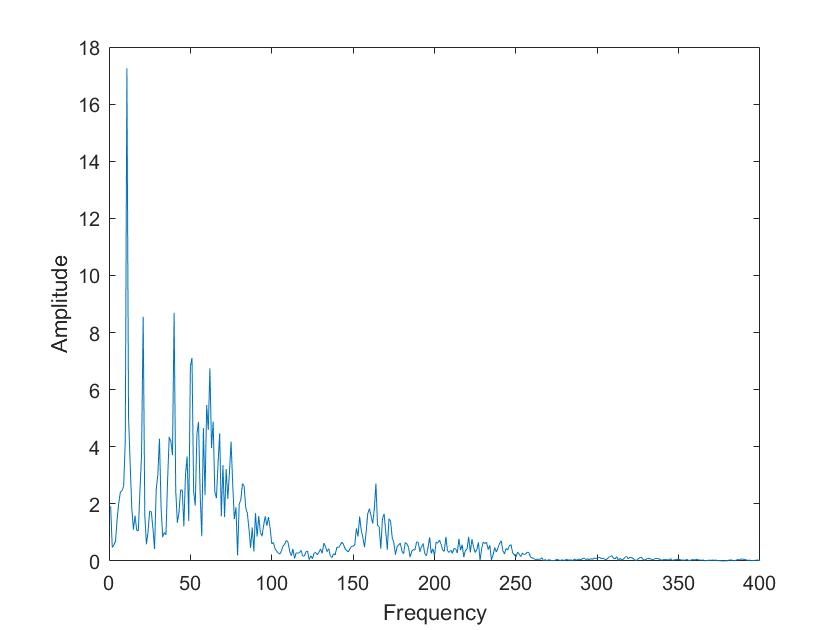
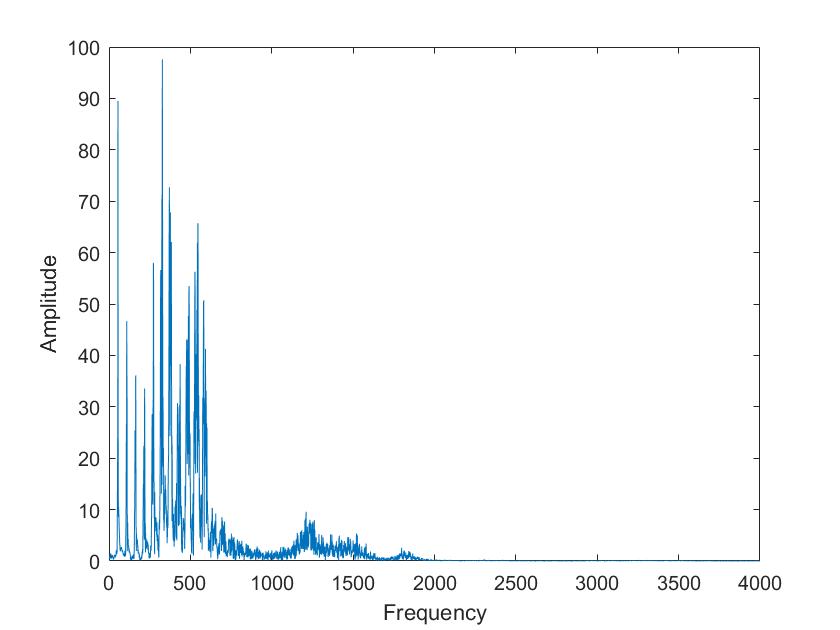
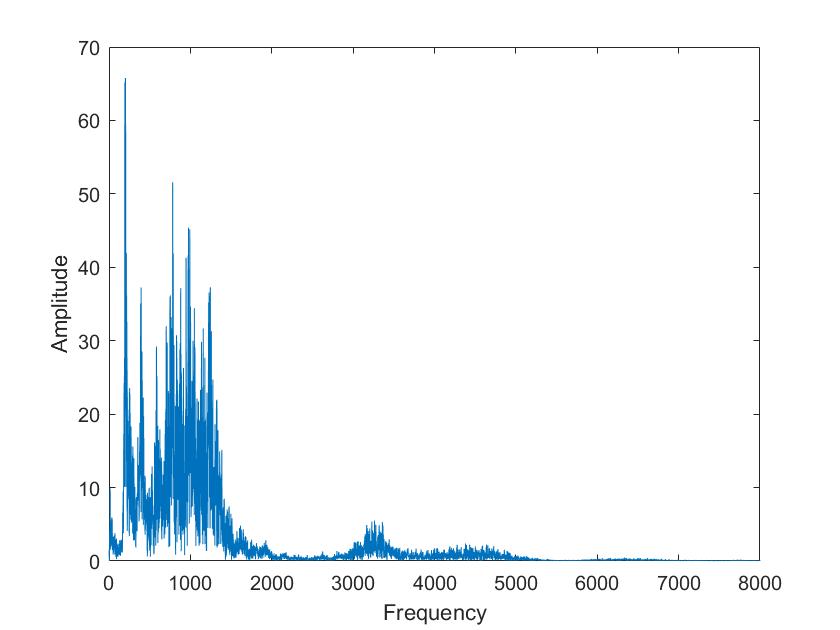
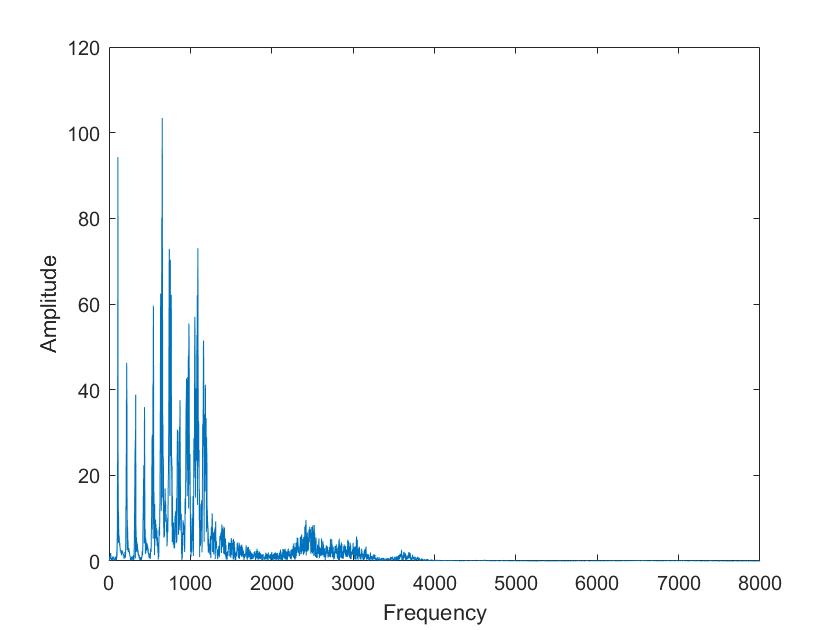
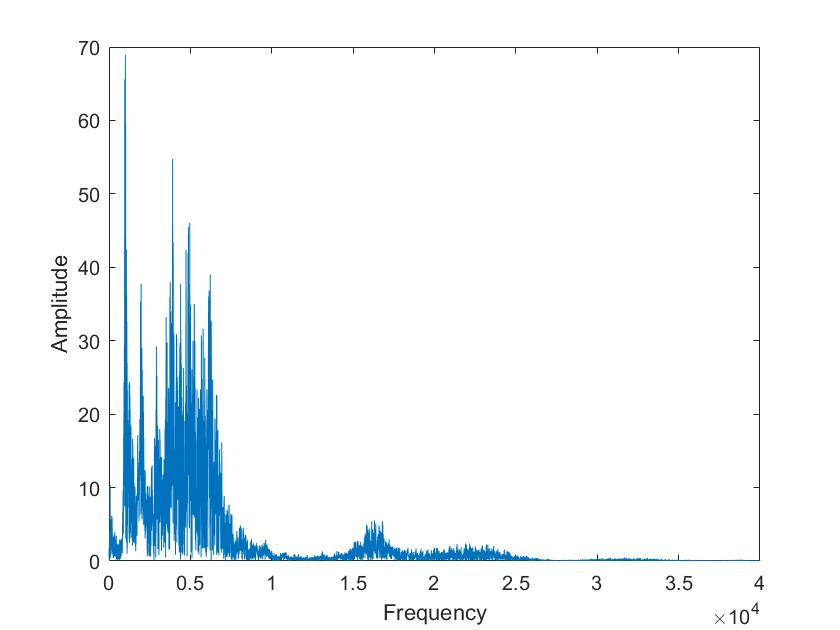
| Mariia a | Tim a |
|---|---|
|
|
|
|
|
|
|
|
|
|
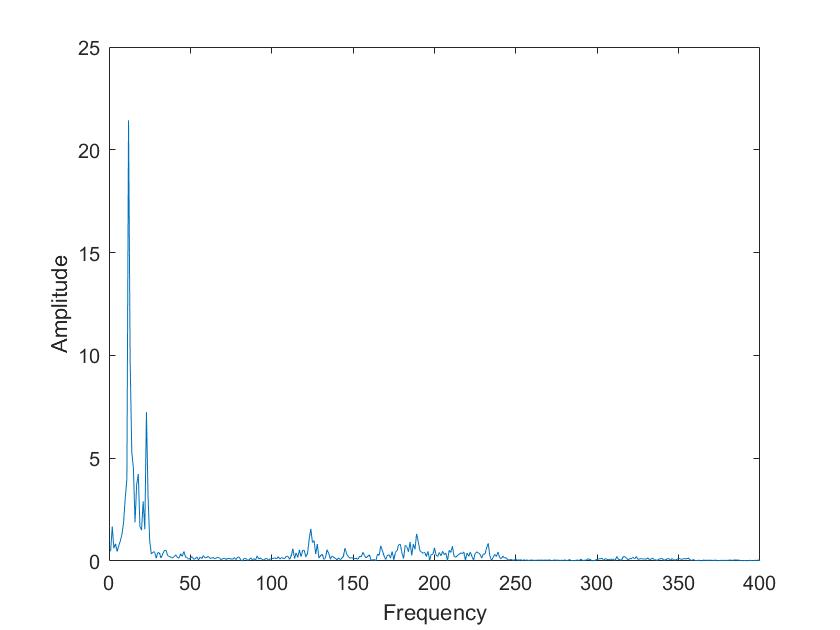
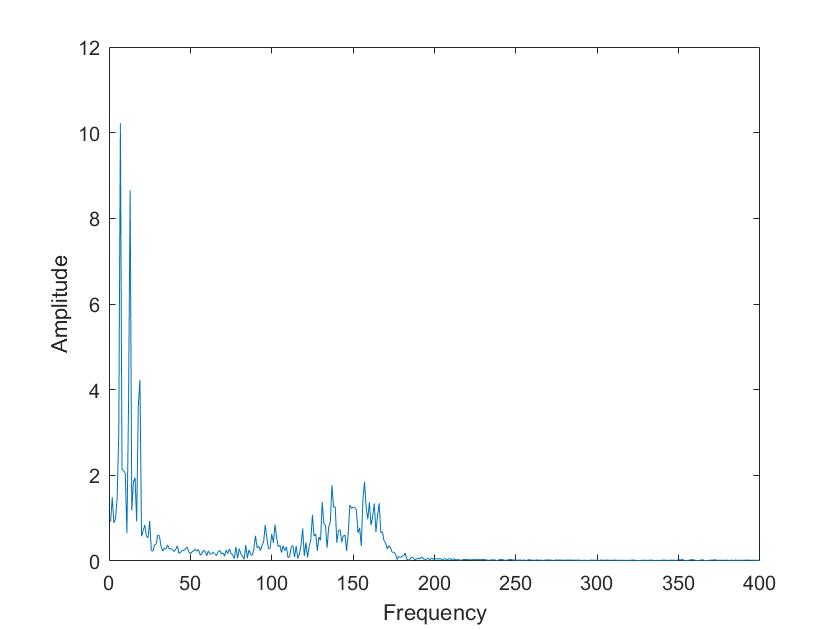
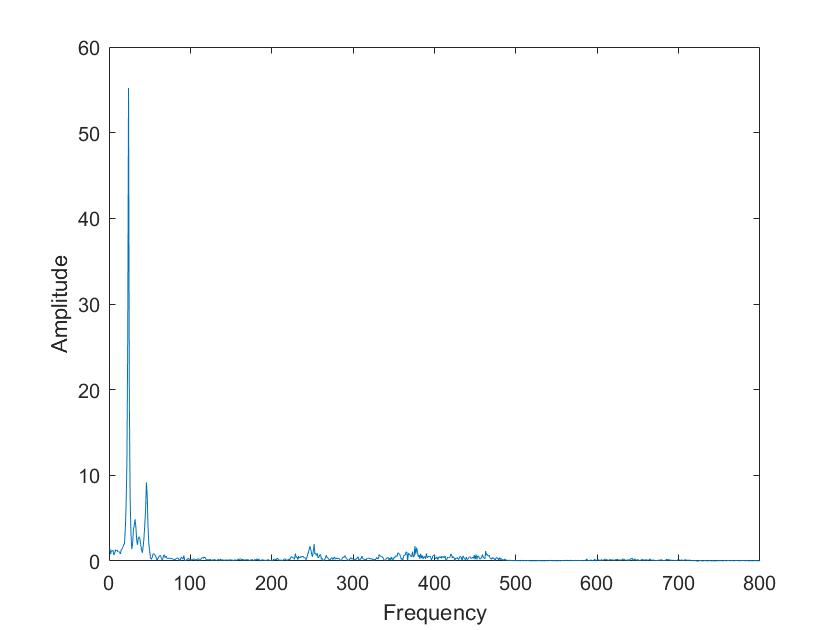
| Mariia i | Tim i |
|
|
|
|
|
|
|
|
|
|
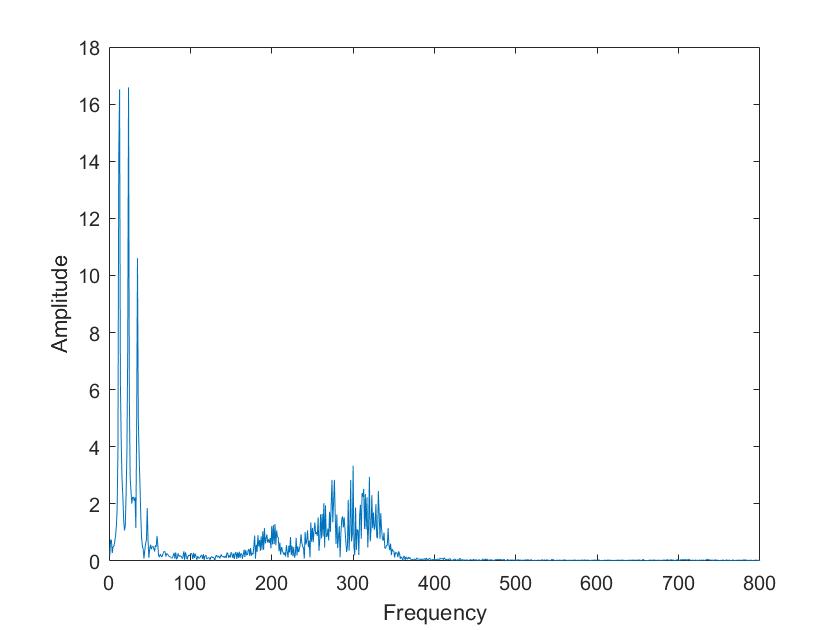
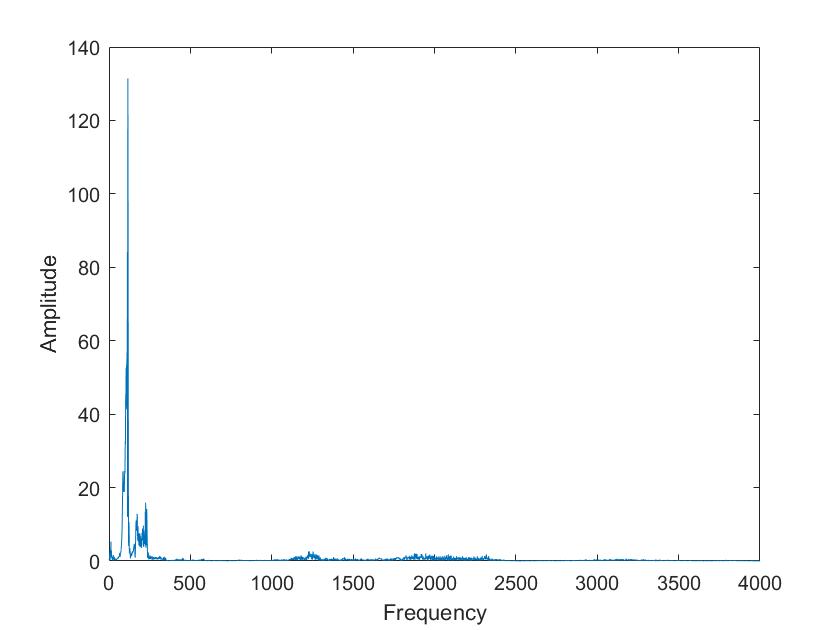
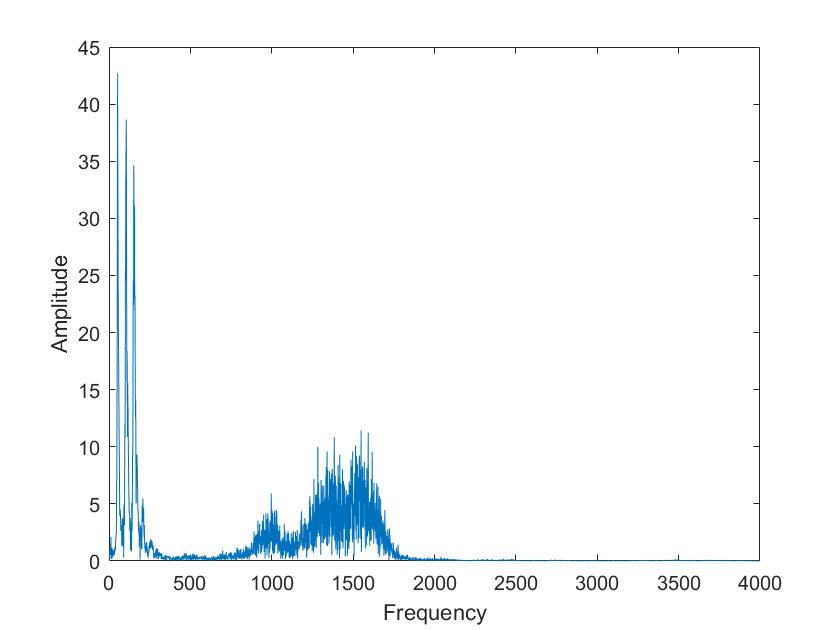
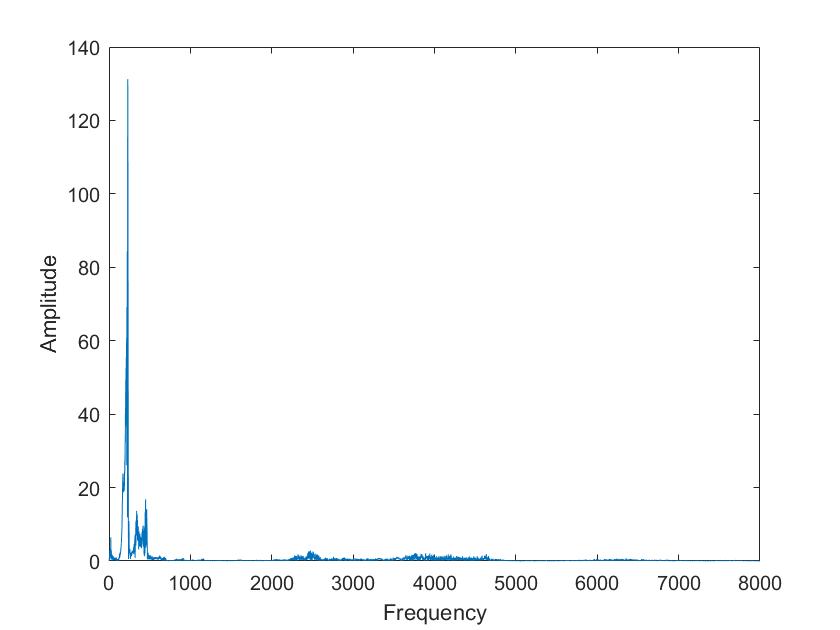
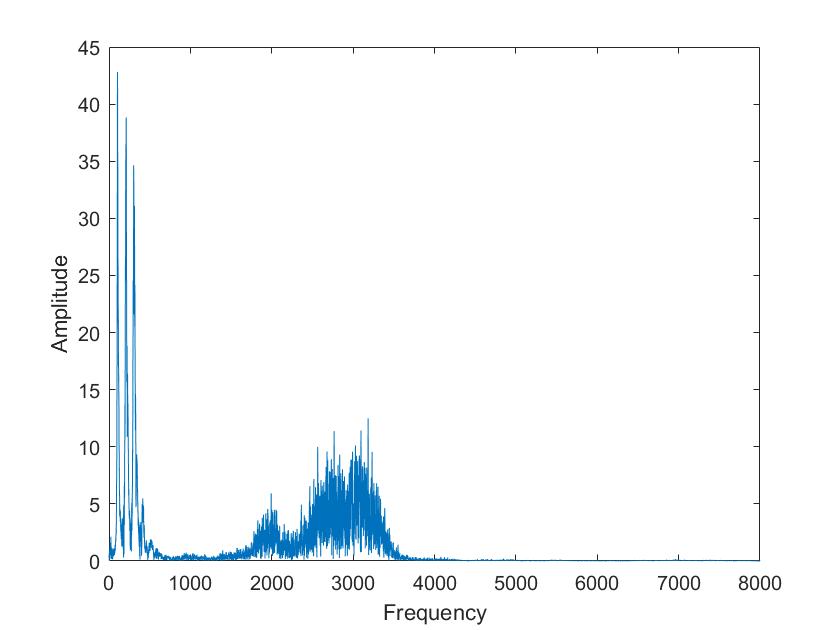
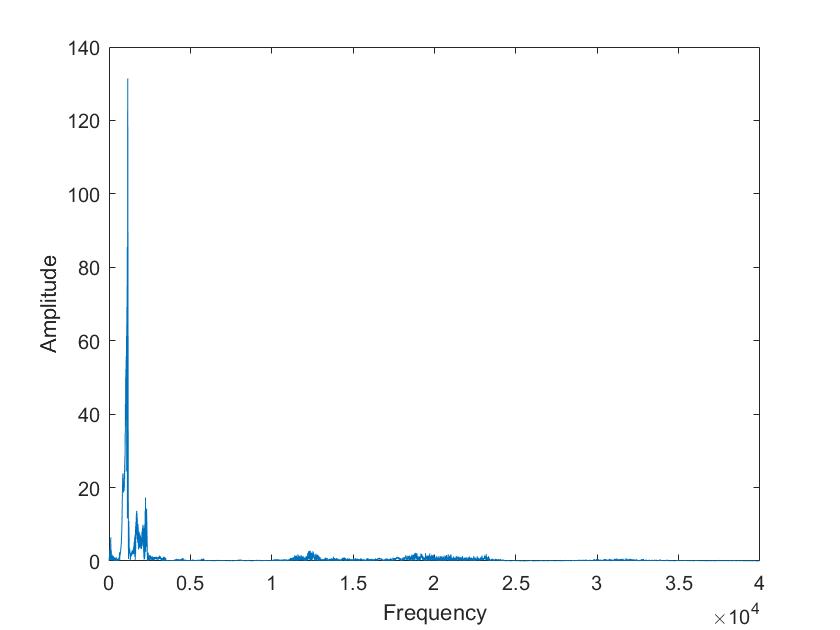
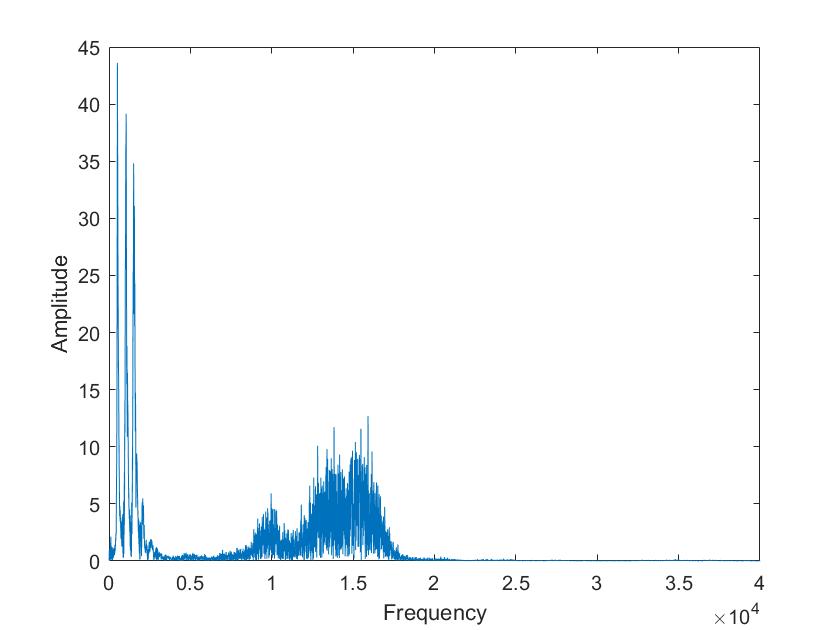
Die obigen Darstellungen sind die FFT transformierten der Sprachsignale von Tim und Mariia, berechnet mit verschiedenen Framelaengen. Die Framelaengen von oben nach unten sind 50ms, 100ms, 500ms, 1s, 5s. Man kann sehr gut sehen, dass die Sprachsignale nicht nur aus 3 Grundfrequenzen zusammengesetzt sind, so wie im obigen Signal, sondern aus einer ganzen Reichweite von Frequenzen.
Im Vergleich der Sprachsignale zwischen Tim und Mariia haetten wir zunaechst erwartet, dass Tims Vokale aus deutlich tieferen Frequenzen zusammengesetzt sind. Dies ist aber nicht sehr eindeutig zu erkennen. Aber man kann eindeutig erkennen, dass seine Vokale aus eindeutigeren, distinkten Frequenzen zusammengesetzt sind als die von Mariia.
Beim Vergleich von a und i ist sehr eindeutig sichtbar, dass das i aus einer deutlich kleineren Reichweite von Frequenzen zusammengesetzt ist. Vor allem bei Mariia, Tim hat noch einen Einfluss hoeherer Frequenzen.